Lines and Planes

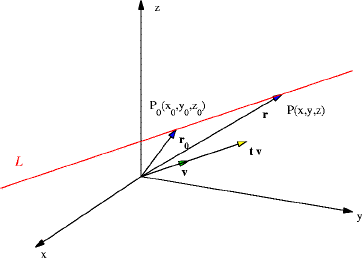
Suppose a point P0(x0, y0 , z0 ) is on a line L and we have a vector v that is parallel to the line L. Let P(x, y, z) be any other point on the line. Set r0 be the vector from the origin to P0 and r be the vector from the origin to P. Referring to the figure below we have that

r = r0 + t v

If v = < a, b, c > then the above equation simplifies to following three expressions

x = x0 + a t    y=y0 + b t   z = z0 + c t

Where t . These are the parametric equations of the line L.

Example

Find the parametric equations of the line through the points < -1, 1, 5 > and < 4, 3, -2 >

We first find the vector joining these points, since that is the direction of the line. v=< 4, 3, -2 > —< -1, 1, 5 > = < 5, 2, -7 > and so the parametric equations are

x = -1 + 5t    y = 1 + 2t     z = 5 — 7t

One way to describe a plane containing a point P0(x0, y0, z0) is the set of all vectors with initial point P0 and terminal point P(x, y, z) that are orthogonal (perpendicular) to a given vector n. The figure below illustrates this.

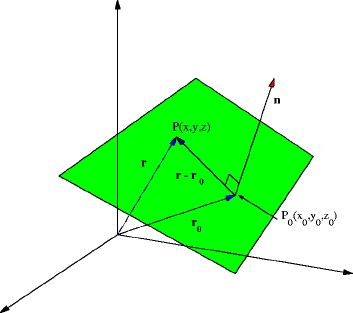
From this diagram we see that the vector n is orthogonal to the vector r — r0. This leads to the equation

n · (r — r0) = 0.

If n = < a, b, c > then the above equation becomes

a(x — x0) + b(y — y0) + c(z — z0) = 0

Collecting terms produces the standard linear equation in the variables x, y, and z.

ax + by + cz = d

where d = ax0 + by0 + cz0. Note that the coefficients of this linear equation are the components of the normal vector to the plan.

Example

Find the equation of the plane containing the points P(1, -1, 2), Q(3, 4, -2), and R(0, 2, -2).

We first need to find the normal vector for this plane. This is done b y finding the vectors u joining P and Q and the vector v joining P and R. These vectors are

u = < 2, 5, -4 >     v = < -1, 3, -4 >

Since these vectors are in the plane, the cross product uv is the normal vector. The cross produce is given by

The equation is then given by

-8(x -1) + 12(y + 1) + 11(z - 2) = 0

-8x + 12y + 11z = 2

Back