Partial Derivatives

Given a function z = f(x, y), it represents a surface in

³ and so a rate of change at a point depends on the direction from the point. We look at these rates of change along lines parallel to the x- and y-axis.

Consider the function l5g1 (1K) at the point (1/2, 1). We calculate the following limits

These limits are the slopes of the tangent lines to the curve f(x, 1) and f(1/2,y) respectively and are called the partial derivative of f with respect to x at (1/2, 1) and the partial derivative of f with respect to y these are denoted by f_x(1/2,1) and f_y. The situation is shown in the graph below. The curves f(x,1) and f(1/2,y) are the traces from the planes y = 1 and x = 1/2 cutting the surface z = f(x,y).

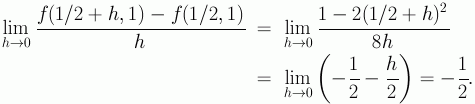
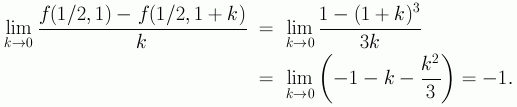
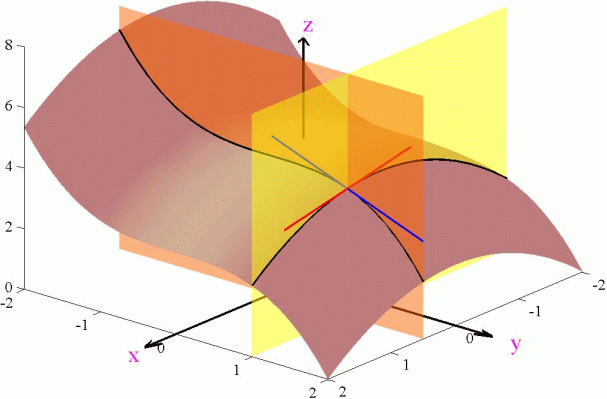
These partial derivatives are calculated in the same way as derivatives are calculated for functions of a single variable with the exception that we treat the other variable as a constant.

f_x, regard y as a constant and differentiate f(x, y) with respect to x.
f_y, regard x as a constant and differentiate f(x, y) with respect to y.

The following example shows this

f(x, y) = x cos(xy)

f_x = cos(xy) + x (sin(xy) y) = cos(xy) xy sin(xy)

f_y = x (sin(xy) x) = x² sin(xy)

Other Notations

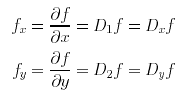
Below is the graph of the function f(x, y) = x e^{(– x² –
y²)} and following that are the graphs of f_x and f_y. Can you tell which is which?

**Partial Derivatives**

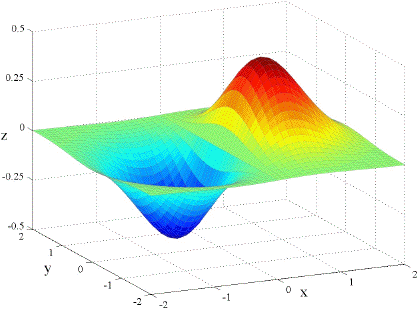
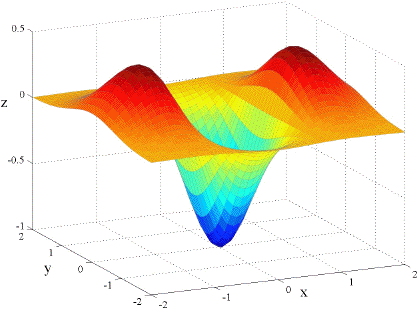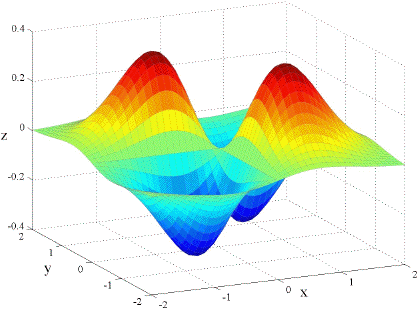There are higher order derivatives these have the notations

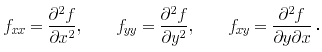
It should come as no surprise that if the partial derivatives are all continuous then f_xy = f_yx. Below are the graphs of f_xx, f_yy, and f_xy for the function f(x, y) = x e^{( x² y²)}

f_xx	f_yy

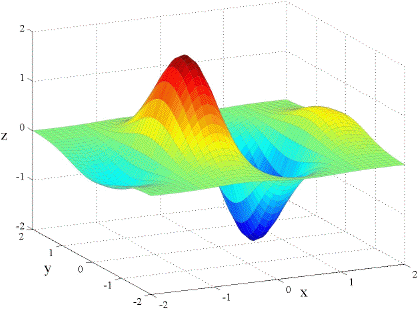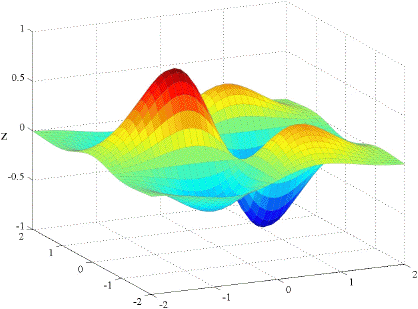f_xy

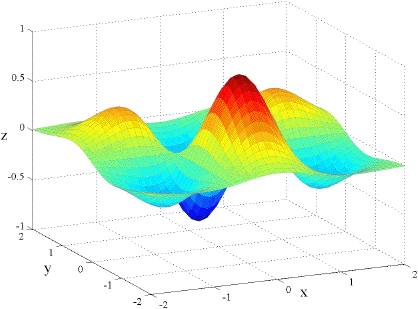Back