Tangent Planes and Linear Approximation

We first reconsider another way to define derivative for a function of one variable. Recall a function L : n is a linear function if for any x, y n and any r ,

L(x + y) = L(x) + L(y)

L(rx) = r L(x).

In this case f must have the form

for some vector c n

Suppose f is a function of one variable.

Definition
A function f(x) is differentiable at the point x = a if there is a linear function L(x) such that

Since L(x – a) = c (x – a) then the above definition becomes

So the linear function L is given by f '(a)(x – a). This tells that the linear approximation (tangent line) f(a) + f '(a)(x – a) estimates f(x) for values of x near a. This tangent line is given by

f '(a)(x – a) – (y – f(a)) = 0.

Consider the vector n = < f '(a), ­ 1>. For the function f(x) = x2 at the point a = 1. We have f '(x) = 2x so the tangent line is given by 2(x – 1) – (y – 1) = 0 or y = 2x – 1 and the vector n is  < 2, -1 >. Below is the graph of y = x2, the tangent line, and the vector n drawn at the point (1, 1).

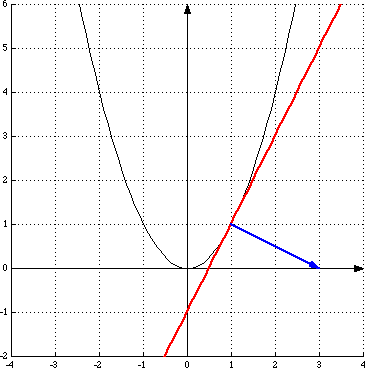
It is seen that the vector n is orthogonal to the tangent line.

Suppose f is a function of two variables.

Definition
A function f(x, y) is differentiable at the point (x, y) = (a, b) if there is a linear function L(x, y) such that

Taking L(x – a, y – b) = c1 (x – a) + c2 (y – b) and y = b we have, assuming x > a, we have

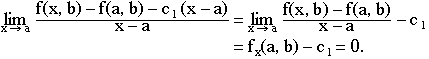
Thus c1 = fx(a, b). In the same way it is shown that c2 = fy(a, b). This tells us that the linear approximation (tangent plane) f(a, b) + fx(a, b)(x – a) + fy(a, b) (y – b) estimates f(x, y) for values of (x, y) near (a, b). The tangent line is given by z = f(a, b) + fx(a, b)(x – a) + fy (a, b)(y – b), or in the standard form:

–fx(a, b)(x – a) – fy(a, b)(y – b) + (z – f(a, b)) = 0.

This shows that the normal vector to the tangent plane is given by

n = < –fx(a, b), –fy(a, b), 1 >

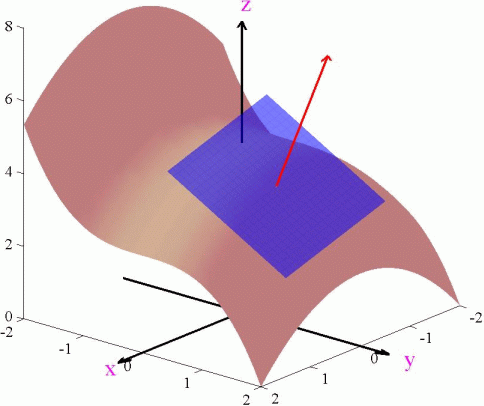
Consider the function at the point (1/2, 1). We have fx(x, y) = -x and fy(x, y) = -y2. Thus the normal vector to the tangent plane is n = < 1/2, 1, 1 > and the equation is 1/2(x – 1) + (y – 1) + (z – 101/24) = 0 or

.

The graph of this plane and the normal vector is shown below.

Back